一部書き換え(グラフを含む)ました(2020.1.4)。
備忘録も兼ね、とにかく分かりやすい例を挙げます。説明も十分にしますので、少し前に書いた記事を参照しながらお読みください。
なお、この記事に直接関連した内容の書籍をブログ管理人が出版しました。記事をリファインして、極力詳しく解説しています。見ていただけるとうれしいです(2022年5月15日(日))↓
N=100点のサンプリングデータを相手にするとします。データは1秒分と仮定します。前のFFTの記事によると基本周期はT=1秒、基本周波数f=1/T=1Hz。第k次高調波の周波数はfのk倍、つまりkHzです。N点のデータを相手にする場合、FFTでは第1次、第2次、……、第N次高調波の周波数が求まります。このとき第N次高調波の周波数はサンプリング周波数、つまりfsヘルツです(今回の場合、第N次高調波はNヘルツ)。そのうち意味があるのはN/2次未満以下なのでした。(2022.1.25修正)
以下のコードを実行してみましょう。
import numpy as np
import scipy as sp
from scipy.fftpack import fft
import matplotlib.pyplot as plt
from matplotlib import pyplot
pi = np.pi
fs = 100 #サンプリング周波数
N = fs #サンプル数はfsとする
t = np.arange(0, 1, 1/N) #1/N秒刻みの時刻の配列。基本周期T = 1。
y = np.sin(2*pi*4*t)+2*np.sin(2*pi*10*t) #周波数は4Hz,10Hz
pyplot.plot(t, y) #元の波形を描画
pyplot.show()
#yf[k]には第k次高調波のフーリエ係数が入る
yf = sp.fftpack.fft(y[:N])
pyplot.plot(t, np.abs(yf)) #含まれる周波数成分を描画
pyplot.show()
yif = sp.fftpack.ifft(yf[:N]) #ifftで元の波形に戻してみる
pyplot.plot(t, yif) #戻ったか、確認。最初と(一応)同じグラフ。
pyplot.show()
yf[10] = 0 #第10次高調波をカット
yf[N-10] = 0 #第10次高調波をカット
#t = np.arange(0, 1, 1/N)
#1/N秒刻みの時刻の配列。基本周期T = 1。
yif = sp.fftpack.ifft(yf[:N]) #その波形を求める
pyplot.plot(t, yif)
pyplot.show()
plt.plot(t, np.abs(yf)) #周波数成分を調べる
plt.show()
これが元の波形です。↓

FFTで周波数成分が分かります。

右端は第N次高調波、つまり fs ヘルツ(サンプリング周波数)の成分です。今回の場合、100Hzです。例えば横軸の0.4のところにピークがあればそれは40Hzです。左下を拡大すると
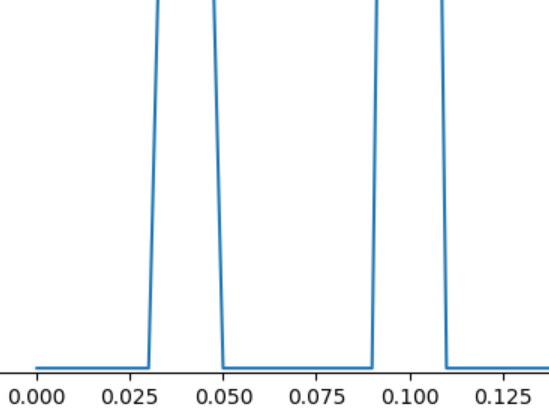
4Hz、10Hzのところに成分が出ていますね。FFTの結果、yf[k]には第k次高調波の成分が入ることを思い出し、IFFTで第10次高調波をカットして波形を見てみると……
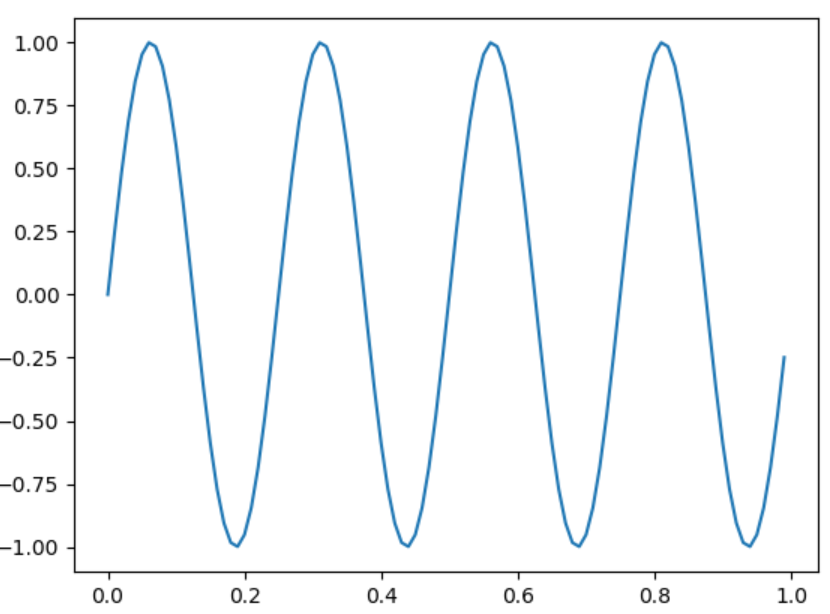
単純なサインカーブになりました!! これの周波数成分をFFTで調べると……

10Hzの成分は消えたようです。左下を拡大します。
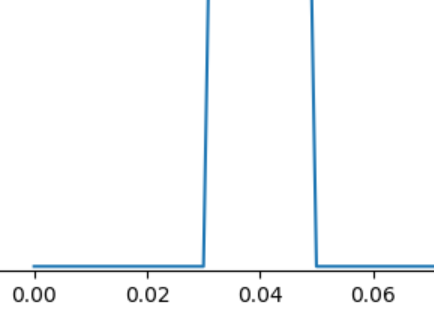
4Hzのところに成分が出ています。
波形、周波数成分が目で見て分かるよう、よいパラメータを見つけて実行してみました。例えばNを大きくすると刻みも短くなって滑らかなグラフになりますが、十分拡大しないと周波数成分がはっきりせず、「分かりやすい」例としてはうまくありません。そこでN=100で手を打ちました。
終わりにあと少しだけ大事な説明をします。第10次高調波をカットするために
yf[10] = 0 #第10次高調波をカット
yf[N-10] = 0 #第10次高調波をカット
としました。FFTではyf[10]に第10次高調波のフーリエ係数が入りますが、フーリエ係数はもともと複素数です。FFTの性質で、第k次高調波のフーリエ係数 yf[k] は yk[N-k] の共役複素数に等しい、というのがありました。だから、今回のようにフーリエ係数をいじって元の波形に変更を加えようとするときは、

が成り立つようにしなければなりません。今回は単に第10次高調波をカットするだけなので、yf[10] = yk[N-10]=0 とすればOKです。実際、このとき上の式は成立します。
