この記事に直接関連した内容の書籍をブログ管理人が出版しました。記事をリファインして、極力詳しく解説しています。見ていただけるとうれしいです(2022年5月15日(日))↓
前回、FFTの例をお見せしました。さらに理解を確実なものにするため、もう少し別のパラメータで確認してみましょう。タイトルは「FFTとIFFT」となっていますが、今回はFFTのみで説明します。コードは以下の通りとします。
import numpy as np
import scipy as sp
from scipy.fftpack import fft
import matplotlib.pyplot as plt
from matplotlib import pyplot
pi = np.pi
#基本周期T = 3秒。基本周波数=1/3Hz。
fs = 40 #サンプリング周波数。データ1個で1/40秒。
N = 120 #データ数は3/(1/40)=120
#tは1/40秒刻みの時刻の配列。1/40秒ごとに3秒間、サンプリング
t = np.arange(0, 3, 1/40)
y = np.sin(2*pi*4*t)+2*np.sin(2*pi*10*t) #周波数は4Hz,10Hz
pyplot.plot(t, y) #元の波形を描画
pyplot.show()
#yf[k]には第k次高調波のフーリエ係数が入る
yf = sp.fftpack.fft(y[:N])
pyplot.plot(t, np.abs(yf)) #含まれる周波数成分を描画
pyplot.show()
データ数は120です。するとFFTでは第120次高調波まで得られます(が、そのうち意味があるのは第59次高調波までなのでした)。この音をT=3秒、流しています。このTが基本周期です。すると基本周波数はf=1/T=1/3Hzです。第1次高調波、第2次高調波、第3次、第4次、……、第120次高調波の周波数は順に1/3Hz、2/3Hz、3/3Hz、4/3Hz、……、120/3Hz=40Hz(=fs)です。だから、得られたFFTの結果の横軸にはこれらが目盛られていると考えます。横軸の左端は0Hz、右端は40Hz(=fs)です。
元の波形はこれです。
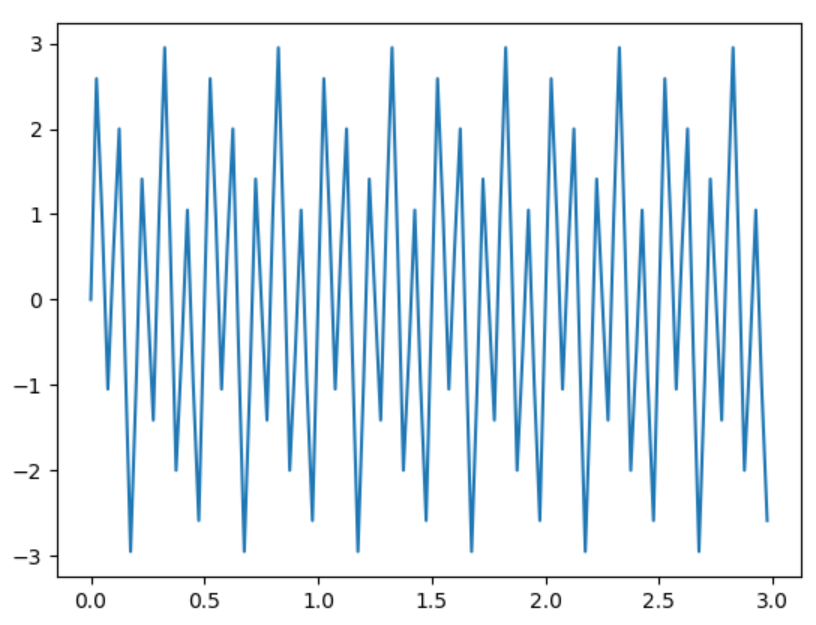
これに対してFFTを実行すると次のようになります。

右端の「3.0」のところには120/3=40Hzの成分(=0)が現れています(第120次高調波の周波数です)。例えば「2.5」のところには単純に比例配分して40×(2.5/3.0)=33.3Hzの成分が現れます(これも0ですが)。
左から2つ目のピークは、拡大すると以下の通りです。

「0.75」のところのピークの周波数はやはり単純に比例配分して40×(0.75/3)=10Hzです。これがコード通りの10Hzのピークなのです。
まとめましょう。
データ数をN、それだけの音が流れるに要する時間をT秒(従って基本周波数は1/Tヘルツ)とするときのFFTの結果の右端は第N次高調波の周波数成分でfsヘルツ(=N/Tヘルツ)。そこより左側は、単純に比例配分して周波数を求められる。
なお、横軸に周波数を表示させることはすぐできます。右端を40Hz(=fs)にすればよいのですから、コードの下から2行目を
pyplot.plot(t * 40 / 3, np.abs(yf)) #含まれる周波数成分を描画
と書き換えればOKです。以下のように表示されます。

一応、これでFFTの基本的な部分については迷わないはずです。おわかりかとは思いますが、うまくいった例はスニペットとして残しておき、再利用しましょう。
