FFTの話なので、少し慣れていないと分かりづらいかも知れません。過去の記事がありますので、参照して下さい。
画像は縦横がありますが、取りあえず横1列(1行)分の話をしましょう。対象の画像は横1列でNドットあるとします。各点では輝度が決まっています。
![]()
だとしましょう。そして横方向にこのデータが繰り返されていると仮定します。FFTを使いたいので、この仮定が必要です。どの道、時間とは関係ありませんから、周期はN(ドット)と考えます。今までの話との対応を考えるなら「N秒」などと思えばよいのです。FFTによって、基本周波数をf=1/Nとして(単位は「1/ドット」とでも思えばよいでしょう。周期をN秒と考えた人は Hzです)この画像データは
(直流成分)+(第1次高調波)+(第2次高調波)+……+(第N-1次高調波)
と分解でき、高調波の周波数は順に f, 2f, 3f, ……, (N-1)f であることもサウンドのときと同じです。時間が絡んでいなくて、そのために分かりづらくなっていますが今までと同じなのです。ここまで「周波数」という言葉を使っていますが、時間とは関係ないのですから、適切ではないかも知れません。そこで空間周波数という用語を使います。話す側と聞く側がお互いに分かっていればどちらでもよいとは思いますが。
画像データ
![]()
から離散フーリエ係数の定義を用いて
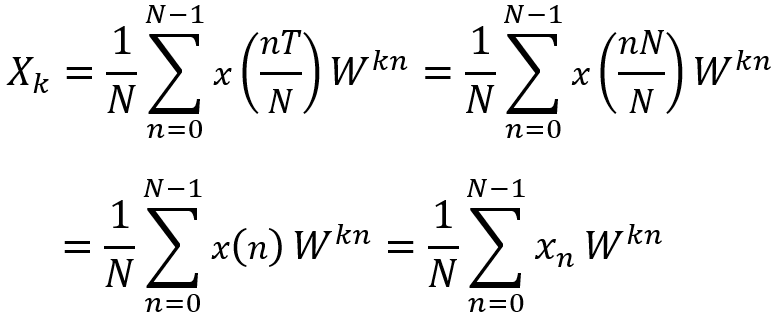
と計算して
![]()
が得られます(もちろんPCならFFTで求める)。それぞれ順に、直流分、第1次高調波、第2次高調波、……に対応する離散フーリエ係数です。
この離散フーリエ係数からそれぞれの高調波の強さが分かります。横1列をザッと眺めて、細かい間隔で明暗が変わる、明暗が急に変わるなどの点が多ければ大きい次数の高調波が強くなります。
画像は縦横がありますから、これだけでは足りません。まず各行(横の並び)について離散フーリエ係数を求め、それを対象にして今度は各列(縦の並び)で離散フーリエ係数を求めます。要するに2回目は離散フーリエ係数を元データとして離散フーリエ係数を求めるのです。こうして画像に含まれる周波数成分を求めます。実際の定義は次の書籍などで確認していただければよいと思います。
ただ、この本には空間周波数については書いてありません。ぼくは他にもいろいろ本を見たのですが、どうもこれが今ひとつ分からず、よく考えてみてはっきりした部分を今回、記事にしました。備忘録です。
