自然数全体の集合をNと書くことにします。N={1, 2, 3, ……}です。Nと1対1に対応のつく集合を可算集合と呼びます。例えば T={2, 4, 6, ……}は可算集合です。NからSへの1対1の対応fを f(n)=2n で定義できるからです。平たく言えば可算集合とは要素を1,2,3,……と数え上げることができる集合です。
さて、こういう問題を考えましょう。
------------------

距離dをどう与えても、平面のどの点に対しても距離がd以下である S の点が存在するように、S の点を平面に配置できるでしょうか。
------------------
要するに平面のどの点のどれほど近くにも必ず S の点が存在するようにして欲しいのです。S は可算集合なので、結局平面に1,2,3,……と自然数を配置するのと同じです。さあ、しばらく考えてみてください!!
…………Thinking Time………………
解答です。自然数nに対して、原点を中心にして1辺nの正方形を描きます。正方形には格子を入れます。幅1/nです。つまり1辺nの正方形を、縦横1/nの正方形で敷き詰めた感じです。図を見てください。
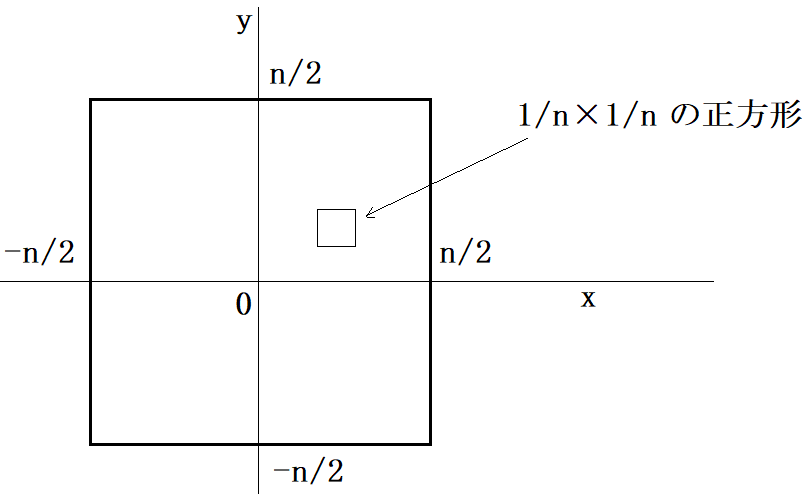
正方形は(n×n)×(n×n)枚あります。これらの正方形に S の点を1点ずつ置くことにします。正方形内ならどこでもOKです。この操作をn=1,2,3,4,……に対して実行するのです。n回目までで点は
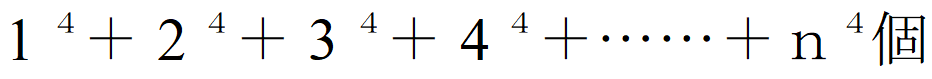
ですから、Sの点が足りなくなることはもちろんありません。また、例えば(13, 20)という点の近く、例えば距離1/100以下にSの点は存在します。n=200とでもすれば正方形は1辺1/200、もちろん(13, 20)を含む正方形がありますが、対角線の長さ(√2)/200なのでSの点の配置の仕方から距離は(√2)/200以下、従って1/100以下です。
この類いの問題は結構好きで、気が向いたらまた書いてみます。