通勤先の最寄り駅から学校まで、バスを使っていたことがあります。ある朝のこと。生徒はあまり使わないのですが、その日はたまたま女生徒が7,8人乗っていました。早い時刻ですし、しかも女子だし、まあ多分きっちりした真面目な生徒でしょう。学校に一番近いバス停までは10分くらいです。ぼくは本を読んでいたのですが、ふと気づくといつもと景色が違います。「??」と思ってよく見ると、もう降りるはずのバス停は過ぎていました。仕方なく次のバス停で生徒たちと一緒に降りて歩きました。
ぼくはほとんど「降ります」のボタンを押したことがありません。まず大抵、誰かが押してくれるからです。しかし全員ボタンを押し忘れなんて珍しいこともあるもんだ、と歩きながら思ったのですが……。よく考えてみるとおかしいのです。生徒はA、B、……、Gの7人とし、「生徒Aがボタンを押し忘れる」という事象をA、「生徒Bがボタンを押し忘れる」という事象をB、……で表します。この日、事象A∩B∩……∩Gが起こったのです。それぞれの生徒が押し忘れる確率は大きく見積もって1/20とします。真面目な子たちですし、実際にはもっと小さな確率だと思います。このときA∩B∩……∩Gの起こる確率は、
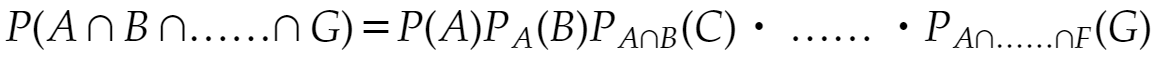
で計算できます(確率の乗法定理)。右辺の7個の確率はそれぞれ1/20としてよいでしょう。例えばA∩Bが起こっているとき、Cの起こる確率は1/20ですよね(A∩Bが起こってもCの起こる確率には変化はなさそう)。結局求める確率は1/20の7乗です。これはおよそ0.0000000008です。大体10億分の1程度。宝くじどころではない、大変なことが起こったのです!!!
実は、こうした場合、単純に乗法定理を使っていいのか、そしてそれぞれの確率を1/20と考えてしまってよいのか、どうもぼくにははっきりしません。これが「火星に鶏がいる」と「火星に鳩がいる」だと一方が起これば他方は起こりやすいと考えてよいでしょう。つまり2つの事象は独立ではないのです。でも「Aが押し忘れる」と「Bが押し忘れる」は独立でしょう。つまり事象Aが起ころうが起こるまいが、事象Bの起こる確率に変化はないでしょう。だから確率は単純にかけてよいはず……と思うんですが、やはりモヤモヤしています。誰か教えてください!!!
確率については、大学では週に1回、1学期分勉強しただけです。もっとしっかりやっておけばまた違ったのかも知れません。事象の独立とは違う話ですが、「2つの試行が独立」とは2つの試行の結果の事象がA、Bのとき、A、Bがともに起こる確率がそれぞれの試行でA、Bの起こる確率の積で求まるときを言う、といった説明が高校の教科書には載っています。でもかけていいかどうか分からないのに試行が独立かどうかなんて分かりませんし、少なくとも教科書の説明は不十分です。大学の先生はこの辺を一応はっきり説明してくれていました。今回のバスの話も何かスッキリした説明があるのかも知れません……。