そろそろ、複数枚の写真をPCに渡し、写っている立体を再現する実験をやってみたいと考えています。順番にその準備をブログでしてゆきます。
まずは一般逆行列です。Ax=bからxを求めるのですが、方程式の本数が多過ぎたり、少な過ぎたりしても何とかxを計算できます。実用では例えば観測の手間や費用など、いろんな事情で方程式が理想通り手に入らないことだってあるでしょう。そういうときでもそれなりのxが求められるのです。
まずは必要な知識をまとめておきましょう。∇fを次で定義します。

∇は「ナブラ」と読み、x、y、zの関数から3次元のベクトルを作る働きを持ちます(4次元でも5次元でも同様)。

このとき以下が成立します。なお、ベクトルx,yの内積を(x,y)、あるいはx・yで表しています。
∇(x,a)=a ……(1)
Aが対称行列のとき、
∇(x,Ax)=2Ax ……(2)
(1)は

から、(2)は

からすぐ分かります。また
(Ax,b)=(x,A' b) ……(3)
も成立します。これは内積についての基本的な公式です。成分で考えれば分かります。なおA' はAの転置行列です。
さて、Ax=b ……① を解きましょう。ここで、Aはm×n行列(m>n)、rank(A) = r = n であるとしておきます。つまり、連立方程式と見たとき式の本数が変数の数より多く、Aの列は線形独立です。式が多すぎるのですから、厳密に①を満たすxはありません。だから、次善の策としてなるべく①をよく満たす解を求めることにします。
J=(Ax-b,Ax-b) とおきましょう。これを最小にするxが求められればよいですね。

ですから、
∇J=2A'Ax-2A' b
これを0とおけば
2A'Ax-2A' b=0
A'Ax=A' b

これで x が求まりました。式変形には(1)~(3)を使っています。
(Aはm×n行列なのでA'Aはn×n。ランクに関する公式rank(A) = rank(A'A)と、問題の仮定 rank(A) = n から rank(A'A) = n。よってA'Aは正則)
この

また、n>m=rのときはxは一意に決まりませんが、その中の|x|が最小のものを求めたりします。さっきと近い議論をして
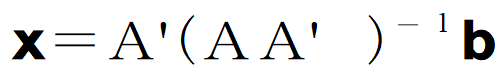
が導けます。この

も一般逆行列です。状況によって形が変わるのです。