ニュートン法でルート3を求める - いぬおさんのおもしろ数学実験室

　微分法を使った、解の近似値を求める方法を説明します。ニュートン法と言います。ここでは $x^{2}－3＝0$ の正の解を求めてみましょう。これはつまり、 $\sqrt[]{3}$ を求めることになります。
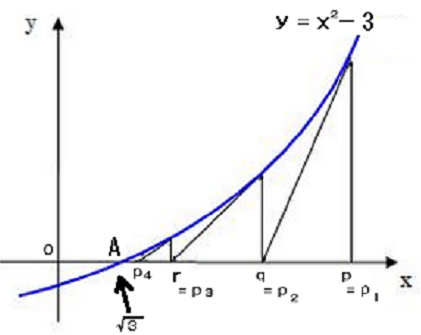
　まずｙ＝ $x^{2}$ －3のグラフ上の、ｘ＝ｐでの接線の方程式を求めます。ｙ’＝2ｘですから、公式（教科書に載っている）からｘ＝ｐでの接線はｙ－( $p^2$ －3)＝2ｐ(ｘ－ｐ)となります（傾きは2ｐで、(ｐ， $p^2$ －3)を通るから）。これとｘ軸の交点のｘ座標をｑとすると、ｘ＝ｑ、ｙ＝０を代入して－( $p^2$ －3)＝2ｐ(ｑ－ｐ)。これよりｑを求め、
q = (1／2)(p + 3／p) ……★
を得ます。図の点Ａはｘ座標が $\sqrt[]{3}$ ですから、ｐよりｑの方が $\sqrt[]{3}$ に近いですよね。もう1回、今度はグラフ上のｘ＝ｑの点で接線を引いて、接線とｘ軸の交点のｘ座標を求めればさらに $\sqrt[]{3}$ に近づきます。★は、あるｘ座標から、そこで引いた接線とｘ軸の交点を求める、言わば公式なのです。つまり★をもう１回使えばｑをもとにしてｒを求められます。ｒ＝(1／2)(ｑ＋3／ｑ)とやるのです。これを繰り返しましょう。しかし次々に計算されるｘ座標にいちいち変数をｐ、ｑ、ｒ、…などと割り当てるわけにはいかないですから $p_1$ ， $p_2$ ， $p_3$ ，……というように数列だと考えます。
f:id:Inuosann:20191012202452p:plain
電卓で順に計算してみます。 $p_1$ ＝２とすると（適当に決めた）
$p_2$ ＝(1／2)(2＋3／2)＝1.75
$p_3$ ＝(1／2)( $p_2$ ＋3／ $p_2$ )＝(1／2)(1.75＋3／1.75)＝1.732142857
$p_4$ ＝(1／2)( $p_3$ ＋3／ $p_3$ )＝(1／2)(1.732142857＋3／1.732142857)＝1.73205081
実際の値は $\sqrt[]{3}$ ＝1.732050808……なので、たったこれだけの計算でかなりよい近似値が得られたことになります。図でも $p_1$ ， $p_2$ ， $p_3$ ，…と、急速に $\sqrt[]{3}$ に近づくことが分かると思います。
　また★の「3」の部分を5に変えれば $\sqrt[]{5}$ が求まるし、最初の方程式を $3cosｘ－0.5＋x^{3} = 0$ などと置き換えてもｘは求められます。数学や物理などで出てくる方程式にはまず解の公式なんかありません。そもそも解の公式のある方程式など、ほんのわずかなのです。しかしこうして数値計算で解に近い値は得られるわけです。微分法を使わない、2分法というのもあります。解が存在する区間を半分に狭めてゆく方法で、これも効率よく数値計算で解を求める方法です。
　★はぼくはやはり高校生の時に知りました。ルートキーがなくてもルートが求められるんだ！と感動したことを憶えています。