この記事に直接関連した内容の書籍をブログ管理人が出版しました。記事をリファインして、極力詳しく解説しています。見ていただけるとうれしいです(2022年5月15日(日))。↓
もう少しFFTで遊んでみましょう。使う言語は例によってPython です。今回はノイズの混ざったデータから周波数成分を求めます。元のデータは一見グチャグチャなのですが、FFTで正しい周波数成分が分かります。こういうのを見るとFFT(あるいは数学)は凄いなあ、と感心します。コードは、コメントも詳しく書いたので、分かりやすいと思います。
#============================= ''' データ数をN、それだけの音が流れるに要する時間をT秒(従って基本周波数は1/Tヘルツ)とする。このときサンプリング周波数 fs = N/T。FFTの結果は、右端は第N次高調波の周波数成分で、それはサンプリング周波数 fs = N/Tヘルツに等しい。そこより左側は単純に比例配分して周波数を求められる。 ''' import sys import numpy as np import scipy as sp from scipy.fftpack import fft import matplotlib.pyplot as plt pi = np.pi fs = 1000 #サンプリング周波数 N = fs * 4 #サンプル数 t = np.arange(0, 4, 1/fs) #1/fs秒刻みの時刻の配列(4秒間) #100Hz, 200Hz の信号にノイズを混ぜる y = np.sin(2*pi*100*t)+1.5*np.sin(2*pi*200*t)+3*sp.randn(t.size) plt.plot(t, y) #元の波形を描画 plt.show() #yf[k]には第k次高調波のフーリエ係数が入る yf = sp.fftpack.fft(y[:N]) #得られる最大の周波数成分は fs = 1000ヘルツ。 #つまりFFTの結果のグラフの右端は fs = 1000ヘルツの成分。 plt.plot(np.abs(yf)) #含まれる周波数成分を描画 plt.show() sys.exit() #=============================
もとの波形は次の通りです。
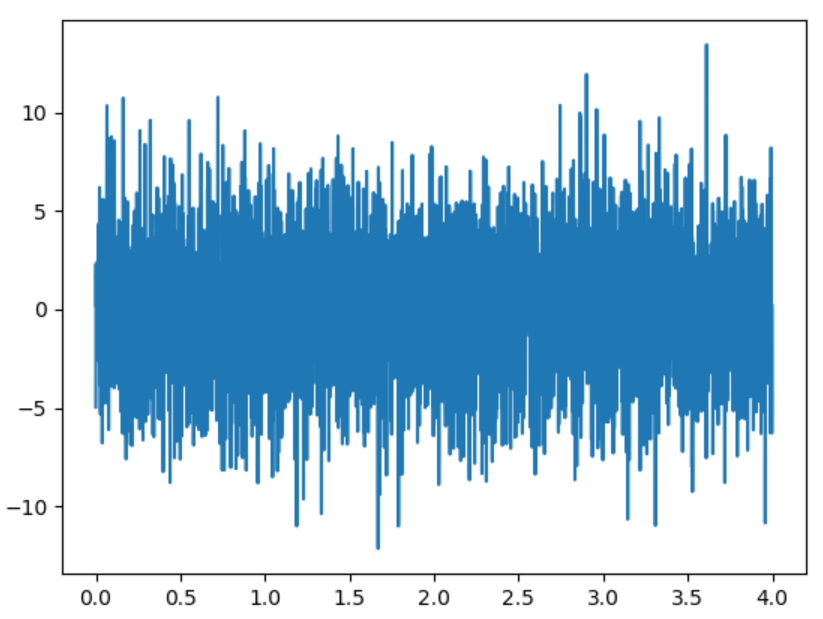
そしてFFTの結果は次。
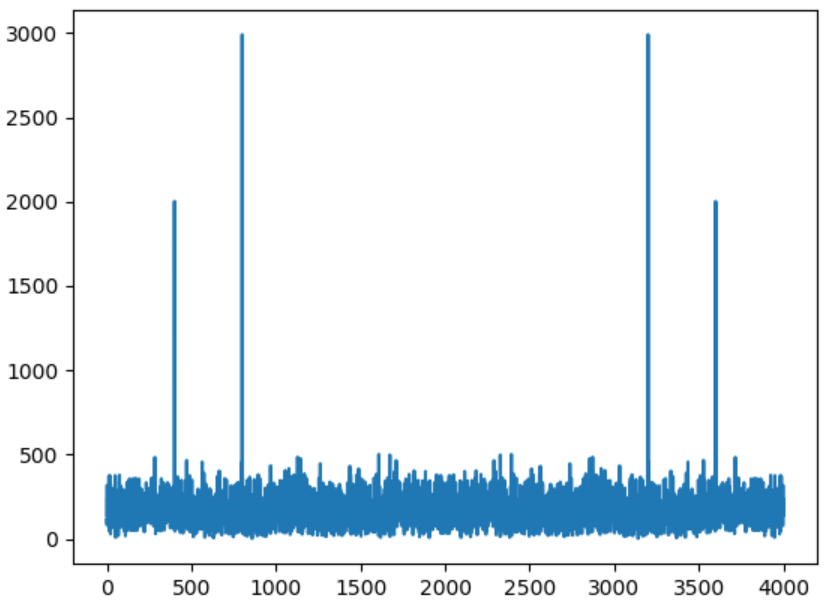
横軸の右端の目盛りは4000になっています。FFTの結果の右端は fs = 1000Hz のはずですから、このままで値を解釈してはいけません。正しいスケールに直します。つまり4で割ればよいのです。左下付近を拡大すると
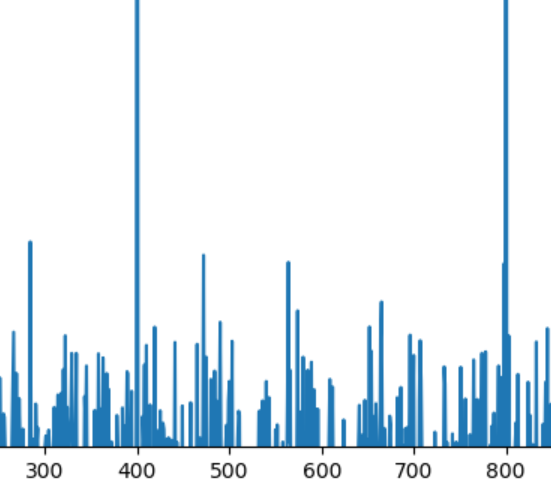
となっています。400,800のところにピークがありますから、先の話通り4で割って100Hz、200Hzの周波数成分が見つかりました。あるいは、最初から正しい横軸を表示すれば問題はありません。以下のようにします。
#============================= import sys import numpy as np import scipy as sp from scipy.fftpack import fft import matplotlib.pyplot as plt pi = np.pi fs = 1000 #サンプリング周波数 N = fs * 4 #サンプル数 t = np.arange(0, 4, 1/fs) #1/fs秒刻みの時刻の配列(4秒間) #100Hz, 200Hz の信号にノイズを混ぜる y = np.sin(2*pi*100*t)+1.5*np.sin(2*pi*200*t)+3*sp.randn(t.size) plt.plot(t, y) #元の波形を描画 plt.show() #yf[k]には第k次高調波のフーリエ係数が入る yf = sp.fftpack.fft(y[:N]) #得られる最大の周波数成分は fs = 1000ヘルツ。 #つまりFFTの結果のグラフの右端は fs = 1000ヘルツの成分。 #■■■ #得られる結果のグラフの横軸は、0~fs(ヘルツ)、要素数は t に合わせる t1 = np.arange(0, fs, fs/t.size) plt.plot(t1, np.abs(yf)) #含まれる周波数成分を描画 #■■■ plt.show() sys.exit() #=============================
「#■■■」で囲まれた部分が書き換えたところです。FFTの結果は以下のようになりました。
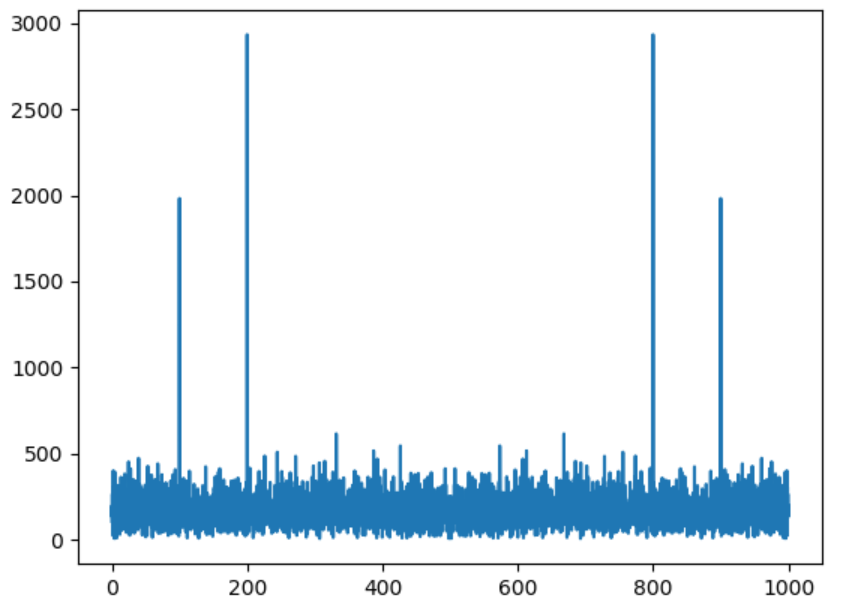
確かに右端が fs = 1000Hzになっていますね。これならひと目でピークが100Hz、200Hzだと分かります。
「ノイズを混ぜる」アイディアは次の本にありました。Pythonの基本、そしてタイトル通り科学技術計算への具体的な応用について書いてあり、参考になります。ブログでも何回も使っているデータプロットツール、Matplotlibについてもまとめてあります。

