区間Iで定義された関数y=f(x)があります。増減表を書くときにいつも使う性質「区間Iで常にf'(x)>0が成立しているとき、関数y=f(x)はその区間で単調に増加する」というのがあります。しかし、導関数の値が正だとなぜ増加なのでしょうか。なおここで「関数y=f(x)は区間Iで単調に増加」とは区間Iの任意の点s、tに対して、s<tならばf(s)<f(t)が成立することです。これは1年生の教科書に出てくる関数の増加の定義です。
導関数の値はその点で引いた接線の傾きなのでした。だから導関数の値がずっと正ならいかにももとのグラフは右上がりになりそうです。……と、高校ではこの程度の説明で済ませてしまうことも多いかも知れません。実際、2年生までの知識ではこのくらいが限度ですし、説明を聞いた生徒も納得します。しかし、上の単調増加の定義に従って「確かに増加だ」と言えるのでしょうか? 曖昧だと言われれば言い返せないでしょう。
ちゃんと示すには平均値の定理を使うのでした。平均値の定理とは……
区間Iで微分可能な関数f(x)があるとき、Iの任意の点s、t(s<t)に対し、s<c<tなるcが存在して f(t)-f(s)=f’(c)(t-s) が成立する
というものでした。区間Iで常にf'(x)>0なら、この定理からIの任意のs、t(s<t)に対してs<c<tなるcがあり、f'(c)>0が成立します。従って f(t)-f(s)=f’(c)(t-s)>0、よって f(t)>f(s) が成立するのです。これはIでf(x)が増加であることを示しています。
あまり厳密に,厳密に……とやると生徒もアップアップしてしまうかも知れませんし、手加減も必要です。でも「関数の増加の定義に従って本当に増加と言えるのか、確認する必要があります。今はそのために必要な道具がないのでやめておきますが」くらいは話してもよいところだと思います。
追加:
極値についてひとつ。極大値とは「グラフで導関数の値が正から負に変わる点の高さ」くらいで、まあまあよいのかも。しかし極値と導関数に直接の関係はありません。極大値は「十分狭い区間での最大値」というちゃんとした定義があるのです。これによれば、下のグラフを持つ関数は点Pで極大値をとることになります。点Pではグラフが尖っていて導関数の値が存在しませんが、そんなことは極値とは関係ありません。
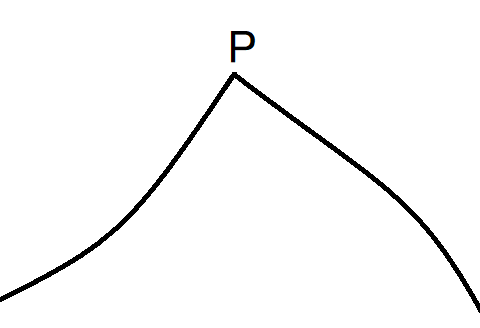
高校で相手にする関数のグラフは定義域全体で微分可能なものも多く、極大値と言えば山のピークみたいになっているものを考えれば大体よいのです。だから曖昧にしてしまってもいいところかも知れませんが、「実は……」と説明しておく方がよいと思います。念のため、下のグラフで「点Pで極大値をとる」と言っても誤りではありません。
