シューティングゲームなどで、敵機に図のような軌道を描かせたいときにどうしたらよいか、考えます。

これだけなら、適当な式を定義してそれに沿って移動させればできるかもしれません。ネットで「いろいろな曲線」などで検索してみてください。「バラ曲線」、「リサージュ曲線」、……いろいろヒットします。曲線のパラメータがいくつもある場合、組み合わせで様々なものが得られることもあります。しかし例えば自由に5点を与え、滑らかな曲線が順にそこを通るようにする(あるいはその5点の辺りを通るようにする)、というのを実現するには別の方法が必要です。ラグランジュの補間法などもよいのですが、図のような曲線を描くのはすぐにはできなさそうです。ラグランジュの補間法についてはこれを参照してください。
また、ベジェ曲線も利用できます。離れたところに曲線が2本あるとき、一応滑らかにつなぐことができます。ベジェ曲線についてはこちらを参照してください。www.omoshiro-suugaku.com
ぼくは実際にベジェ曲線をシューティングゲームで敵機を動かすのに使っています。ただ、状況によっては継ぎ目で速さが「カクッ」と変わり(もちろん理由はあるのですが)、それが目立つときには向きません。軌道の見た目の滑らかさだけでなく、速さも滑らかに変化していないと不自然に感じることがあるのです(こういう「カクッ」という演出をしたいならいいけれど)。また、スプライン曲線というのもありますがこちらはまだ勉強しておらず、今回の目的に使えるか分かりません。
今回、「例えば4点を自由に与え、滑らかな曲線がその4点の辺りを通るようにする」を割と簡単に実現する方法を紹介しましょう。この4点は「制御点」と呼べるかも知れません。やはりこれもシューティングゲームに使っています。与える点は5点でも6点でも(いくつでも)可能です。
4点をP,Q,R,Sとし、位置ベクトルをそれぞれp,q,r,sとしておきましょう。係数をa,b,c,dとし、v = ap+bq+cr+dsで位置ベクトルvを計算します。ここで係数a,b,c,dはキャラクタ生成後の経過時間によって変化させます。
まず関数f(c,h,x)を定義しておきます。
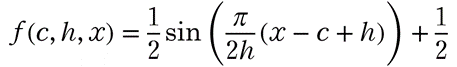
これは例えばc=3, h=1 のとき
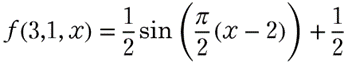
となり、グラフは次のようになります。
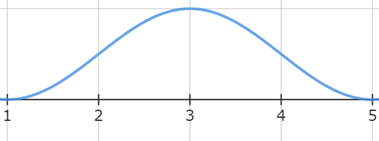
中心(対称の軸)x=c、中心から[グラフの高さ=0]となるxまでの距離が2hであるグラフです。なお、このままだと左右にも波打ちながら伸びてしまいますから、描かれている部分以外はy=0と定義しておきます。cを経過時間に従ってジワジワ増やしてゆくと、グラフが右へジワジワ平行移動します。この関数fを用いて、
![]()
でvを計算し、1点打ちます。fは言わば「重み付け」をしています。ここで
![]()
です。要するに、
![]()
というように係数の和を1となるように調節しながら係数を変化させるのです。この例ではvはqにある程度近い点になるでしょう。cが変わればグラフの中心が変わりますが、係数はそのときのグラフでx=0, x=1, x=2, x=3のときのグラフの高さです。4点はもちろん動きませんが、係数を求めるためのグラフが右へ平行移動するので係数が変わり、vが変化するのです。例えばc=1.7のときは、これはx=2に近いですからrが最も「強調される」ことになります。このように、重み付けのグラフを平行移動しながら点を打ってゆくのです。
なお、Kで割っているのは規格化、つまり無制限に係数が大きくなったり小さくなったりしないよう調整する働きがあります。またhを小さくするとfのグラフの左右の幅が小さくなり、重み付けはシャープ(?)になります。この場合、従って曲線は点p,q,r,sにさらに近い点を通ることになります。
実際に画面のサイズが18×10(座標がこの範囲)のとき、h=0.5、制御点の数を10点で試すといい感じにキャラクタが移動しています。
最初に与える点のうち、隣り合う組が他に比べて距離が近いと、その間ではキャラクタがゆっくり移動するようになります。速さはジワジワ変わるので違和感はありませんが、場合によっては等速がいいと思う人がいるでしょう。さらに工夫すれば可能だと思います。