「1/6公式」というのがあるそうですね。少し前に記事で紹介した
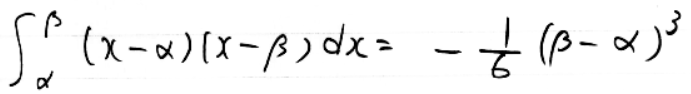
のことだそうです。
「1/6公式」って言うんだ……。昔はそんな名前はついていなかったと思います。まあ知っていた方が便利だから名前もあった方がいいでしょう……。これ、最近の教科書にも載っていた記憶が。「参考」とか「発展」とかで。
次のは「1/12公式」と言うらしいです。
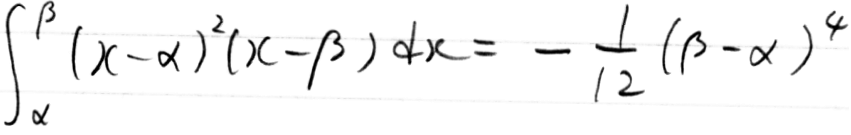
これも記事を書きました。「公式」という形ではないけれど。
やることは前の記事と同じですが、きちんと証明しておきましょう。
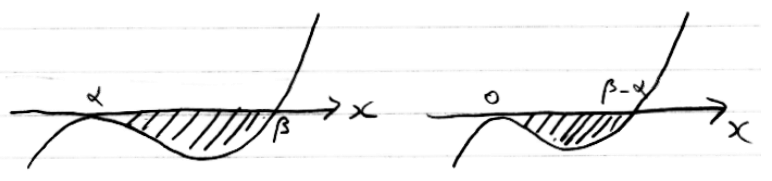
上のグラフの式は左右それぞれ

です。左のグラフをx軸方向へーαだけ平行移動したものです(xをx+αで置き換える)。左のグラフはx=αで接しているのでこういう式になるのです。面積はどちらも同じですよね。だから左の式でx=αからx=βまで積分するのと、右の式でx=0からx=β-αまで積分するのとでは結果は同じはずです。だから次のように計算できます。
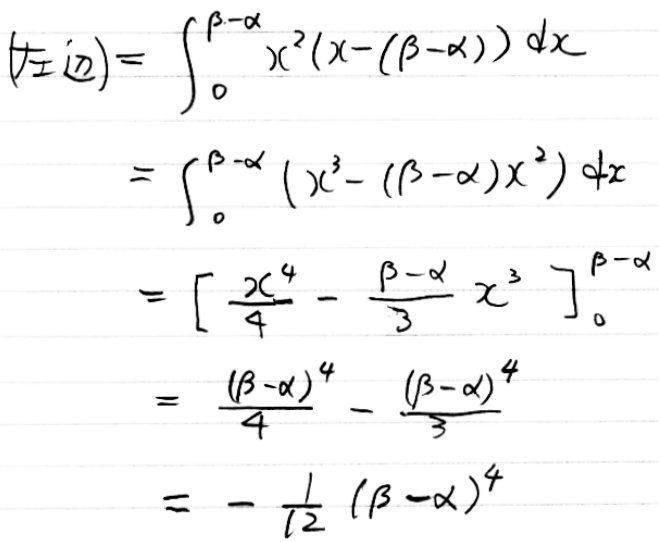
前にも書いたように、x-α=tとおいて置換積分しても同じことです。
どうも、この類いの公式、「大学入試で使ってはいけない」という説があるらしいです。「教科書に書いてあるならいいんじゃないの?」と言いたいですがどっちが正しいのか分かりません。でもハッキリ「ダメ」と言う大学もあるらしい……。意図は知らないし、いわゆる「計算力」も大事だと分かってはいますが、こんな計算、公式で済ませればいいじゃない……。もっと別のことに時間を使いたいのです。これを計算できるかどうかは数学ができるかどうかとは関係ないと思いますし、大事なのは証明を読んだときに理解できるかどうかです。実際、大学で数学を続けられるかどうかは専門書を読めるかどうかにかかっているのです。
しかし「1/6公式」って名前、何だか違和感が。大学をまとめて言う「GMARCH」や「早慶上理」などを聞いたときの違和感に近い……。