100年ほど前のことです。イギリスのアラン・チューリングという数学者が「チューリングマシン」という仮想的な機械を考えました。コンピュータどころか電卓もない時代ですが、チューリングマシンはある意味、現代のコンピュータと同じ働きをします。たまに「ピラミッドの時代のコロ(丸太などを荷物の下に敷いて荷物を移動させる)と現代の車と原理は同じ」なんて話を聞きます。少々強引でしょう……。しかしチューリングマシンは現代のコンピュータの関係はそんな「まあ、そう言えなくもないよな」なんて話ではありません。チューリングマシンにできないことは現代のコンピュータにもできないのです。
以下、チューリングマシンをTMと略して書きます。TMは本体(有限状態制御部)と、磁気ヘッド、読み可能な磁気テープを持ちます(下のようなイメージ)。
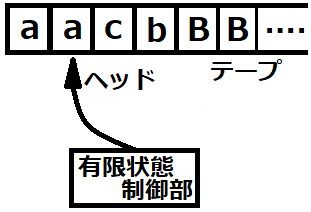
ヘッドはテープに記号を書き込んだり、書き換えたり、消したりできます。テープはマスに区切られており、ひとマスには1個の記号しか書けません。TMはテープを左右に1マスずつ移動させることができます。TMはテープを読み書きしながら様々な計算を実行できるのです。
例えば足し算をするTMがあります。3+4の計算をさせたければ、テープに「111_1111」と書き込んでおき、TM動作させます。アンダーラインは空白の意味です。最初は以下の状態です。▲はヘッドで、先頭の「1」を読んでいます。
111_1111
▲
ヘッドを右へ何回か動かし、次の状態にします。
111_1111
▲
今読んでいる1を空白に書き換え、ヘッドを左へ移動して1を書き込みます。以下のようになります。
1111_111
▲
この動作を何回か繰り返して、もともとあった、1が4個のブロック全体を左へ1マス分、移動して以下の状態にします。次の図は最後の1を書き込んだ直後です。
1111111_
▲
これでTMは停止します。計算結果も出ています。1が7個、並んでいますよね。3+4=7の計算をやったわけです。
何でこんなつまらないことを……と思うかも知れませんが、同じように引き算もできます。かけ算は足し算の繰り返しだし、割り算は引き算の繰り返しだし、従って4則(+-×÷)を計算するTMも作れます。4則ができるともうほとんど何だってできるようになります。与えられた数が素数かどうかの判定をするTM、素因数分解するTM、与えられた数が3で割りきれるかどうかの判定をするTM、……。現代のコンピュータも、CPU(中央演算処理装置。計算はこの部品が担当します)は簡単な計算(4則と、あともっと単純な計算くらい)しかできませんがコンピュータには何だってやらせることができますよね。TMも同じなのです。さらに他のいろいろなTMの動作をマネするTMや、1台あれば他のTMは不要になるTM(万能チューリングマシンと言います)も作れることが証明できます。
さて、そうするともうTMにできないことなんてないような気がしてきます。しかし、チューリングは次の事実を証明しました。
チューリングマシンにデータを与えて動作させたとき、停止するかどうかを判定するチューリングマシンは存在しない
チューリングマシンを見て、「これは止まるよ」とか、「こっちは止まらないよ」とか、判断してくれるチューリングマシンは作れないのです。これは現代のコンピュータでも同じです。つまり以下が成立します。
プログラム(コンピュータ)にデータを与えて実行させたとき、停止するかどうかを判定するプログラムは存在しない
これは「停止問題(halting problem)」と呼ばれています。こうしたことを調べる数学の一分野が「計算可能性の理論」です。ある意味、コンピュータの限界を考えるわけであり、哲学的(?)とも言えますよね。
このような「解けない問題」というのは他にいくつもありますが、それとは別に「解くのが難しい問題」というのもあります。しかしそもそも「解くのが難しい」とはどういうことでしょうか? TMにその問題を解かせると100億年かかる、なんていうことならそれは「難しい問題」と言ってよいでしょう。つまりTMは問題が難しいかどうかの判断の基準にもなるわけです。こうしたことを研究する分野は「計算の複雑さの理論」などと呼ばれます。これを利用して例えば「ある暗号を第三者が解読するのに100億年かかる」といったことが分かれば「安心して使える暗号」ということになりますよね。
この分野、勉強を始めるのに必要な知識は高校でやる数学くらいだし、それに大きな未解決の問題もあるし、意欲のある人は挑戦してみては!? チューリングの名を冠した「チューリング賞」は計算機科学分野で革新的な功績を残した人物に年に1度贈られます。計算機科学界のノーベル賞です。インテル、Googleの支援で、25万ドル(およそ2500万円!)の賞金だそうです!!