すみません、この記事は周辺の知識がないと読みづらいと思います。機械学習、深層学習にソフトマックス関数というのが出てきます。今回はこれを微分したらどうなるか、という話です。ソフトマックス関数は次の通り。
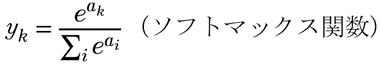
ネットワークの出力層でユニットの値が
![]()
であるとき、ネットワークからの最終的な出力(答え)を上のソフトマックス関数で求めることがあります。これによって入力のベクトルがどのクラスに属するのか判断するのでした。誤差逆伝播法を使うとき、上のソフトマックス関数を偏微分しなければなりません。実は次が成立します。
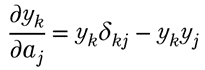
確かめてみます。
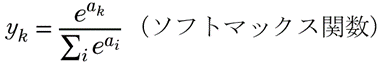
のとき、
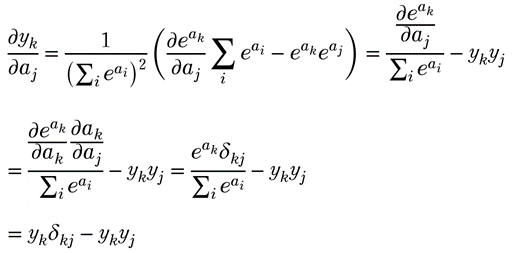
これだけです。途中、
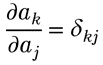
を使っています。
『これならわかる深層学習入門』(瀧雅人2017講談社サイエンティフィク)ではこの式について「確認してみてください」とあり、計算は示されていません。
深層学習、勉強は続けいていますが難しいです。とりあえず、目標を「実験室レベルで画像のクラス認識(犬の画像をPCに見せて「犬」と判断させる、など)をできるようにする」と考えています。
参考にしているのは次のテキストです。
↑ これは今、第2版が出ています。
どちらもよい本だと思います。一方に書かれていて他方に書かれていない(あるいは一方ではあっさり触れているだけ、とか)、ということがいくつもあるように思いますが、交互に読んだりしています。難しいけれど楽しいです。勉強はこうでなくてはいけません!!

