連立方程式を解きます。最初の2本でx、yが決まってしまうので、3本を満たす普通の意味の解はありませんが、なるべくうまい値を見つけます。
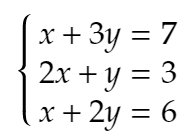
行列、ベクトルを使って考えるため、次のように書き換えます。

後の都合で、これをxp+yq=bと書いておきましょう。つまり
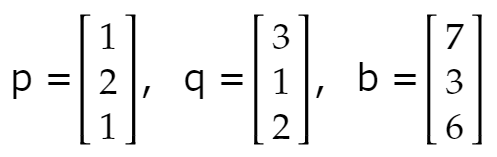
とおくのです。また次のようにおきましょう。
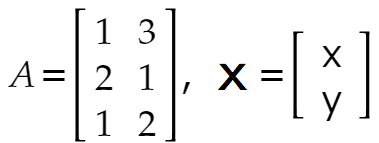
さっきの式はさらに次のように書き換えられます。
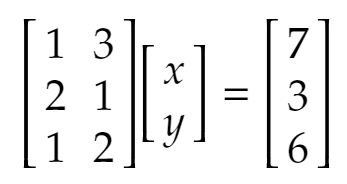
つまりAx=bと書けます。
さて、例えばx=1,y=2としたときの右辺のベクトルと目標のベクトルを比較します。
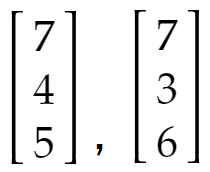
引き算して成分を2乗し和をとると0+1+1=2。この値は小さい方がよいですよね。こうしてx、yを「目標との差のベクトルの成分の2乗の和」が最も小さくなるように定める方法を最小2乗法と言います。
図で説明しましょう。
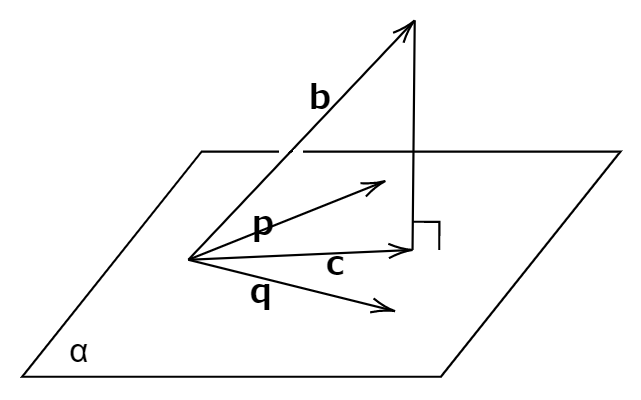
xp+yq=b 、つまりAx=bとうまい具合には行きません。p、qが作る平面α上にbがないからです。そこでbを平面αに正射影したベクトルcを考え、xp+yq=c つまり Ax=c(Ax はα上のベクトル)となるようx、yを定めることにします。「次善の策」ということです。この「次善の策」のxをzと書きましょう。つまりAz=cです。
さて、平面α上のベクトル Axに対し、Ax⊥(b-c) となればよいですね。つまり Ax・(b-c)=0 となればよい。よって Ax・(b-Az)=0。ここから少し変形します。
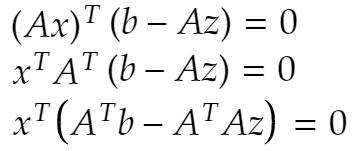
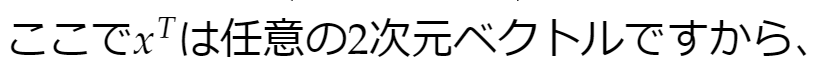

これで「次善の策」であるzが求まりました。
最後、詰めです。この方法では ||b-c|| 、つまり誤差の成分の2乗の和(のルート)が最小になるのでした。つまり、さっきのz=……で出た式が「最小2乗法」による答えです。
この内容は次の本にあります。初めての人に向け、大変丁寧に解説してあります。抽象的な議論でなく、具体的に話を進めています。
記号や説明はこちらの事情であちこち変えてしまっています。何度も紹介している『線形代数セミナー』(金谷健一2018共立出版)にも同様の説明がありますが、(こちらも大変分かりやすいのですが)抽象的な部分があります。記号の扱いに慣れていない方などは今回紹介した本の方がいいかも知れません。
実際にこれを使うのは今回例にした Ax=b をなるべくよく満たすxを求める場面などで、このブログでも写真上の点から空間内の点を求める際に利用しています。でも上の式(z=……)を直接用いたわけではありません。Pythonで一般逆行列を求め、これを使ったのでした。最小2乗法でx、yを求めることは一般逆行列を使うことなのです。上の式(z=……)の中の
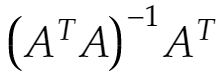
の部分がAの一般逆行列です。
最後に大事なことを。必要があればPythonなどのライブラリを使えばよいのですから、その意味では「今回の内容は知らなくても大丈夫」ということになります。しかしそればかりだと、理論を自分で勉強してゆくことができなくなってしまいます。多分、関係する本を読もうとしても手も足も出ないでしょう。状況次第で仕方ない場合もあるとは思いますが、やはり数学や物理、工学が好きなら自分で一歩一歩理解しながら知識を身につけるのが一番です。
