大学生の時、文系の女の子に卒業論文の相談を受けました。「留学生にいろいろな質問をして、日本人学生と意見が違うということをハッキリさせたい」とのこと。ある質問に対して「はい」と答えるか、「いいえ」と答えるか、調査した結果が以下の表の通りだったとしましょう。
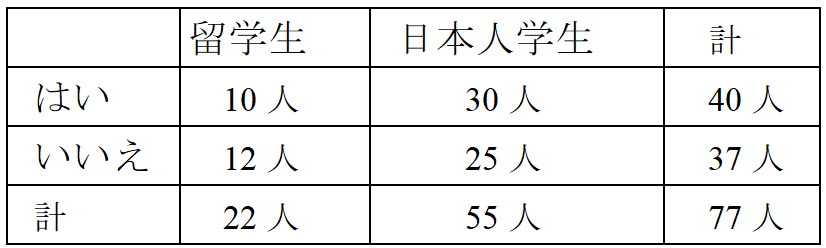
うーん、この はい 10人 30人 40人結果を見るとどうやら「留学生と日本人学生で、『はい』と答える率に違いがある」と言えるような気がします。でも本当にそう判断してしまってよいのでしょうか……?
こうしたことにきちんとした結論を出すため、
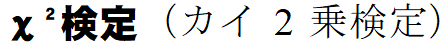
という方法を使います。検定ではまず仮説を立てます。これは正しくないであろうと見込んで立てる仮説で、帰無仮説(きむかせつ)と呼ばれます。無に帰する、というわけです。ここでは
仮説H0:「留学生と日本人学生の間に答え方の違いはない」
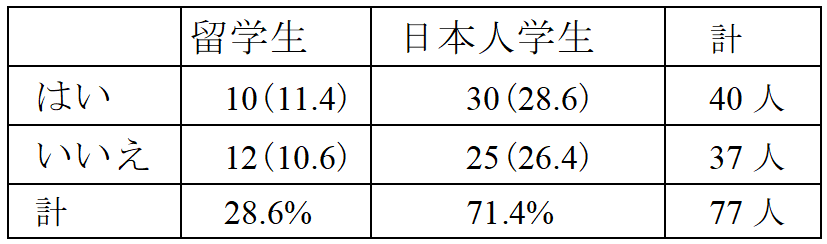
となります。この仮説H0が正しいかどうか検討するのです。下の表には、上の表から計算した数値をいくつか書き加えてあります。留学生22人、日本人学生55人なので、それぞれの比率は22/77=28.6%、55/77=71.4%。「はい」と答えたのは40人なので、仮説が正しければ(留学生と日本人学生の間に考え方の差がなければ)この40人は28.6%、71.4%の比率に分かれるでしょう。つまり40×28.6%≒11.4人、40×71.4%=28.6人。同じように「いいえ」の行にも比率から計算した人数を入れます。()内の数がそれです。言わば期待される人数を計算したわけです。
さて、ここからカイ2乗を計算します。これは期待される値と実現されている値の違い具合を表す量です。
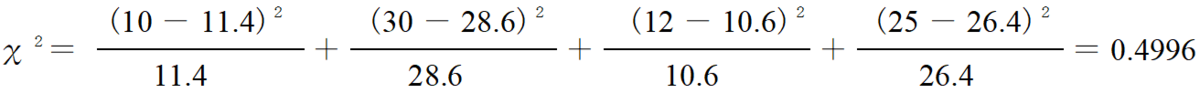
どういう操作をしているのか、分かりますよね? こうして計算したカイ2乗の値が3.841を超えていると「95%の確率で仮説H0は誤りである(仮説H0は棄却(ききゃく)できる)」と判断してよいことが分かっています。3.841というのは「カイ2乗分布表」の有意水準5%、自由度1(※)の欄を見ると載っています。棄却とは捨てること。今、χ2=0.4996≦3.814ですから「仮説H0は棄却できない」ということになります。つまり「留学生と日本人学生の間で考え方に違いがある」とは言えない、と明らかになったのです。
(※)自由度とは……先の表は2×2でした。はい・いいえ、留学生・日本人学生だからです。このとき、(2-1)×(2-1)で計算される量です。例えば3×5の表だったら2×4=8が自由度です。
平均だの割合だの、それっぽいデータを見せられるとなんとなく厳密な気がして、説得されてしまいそうになります。しかし何の説明にもなってないデータだってあるのです。成績が上がっているというデータも実はその証明にはなっていなかったり、遅刻が減っているというデータも実はたまたまだったのかも、ということです。他にもありがちなのは「~~の生徒は成績が低い傾向がある」とか「成績が低い生徒は~~であることが多い」とか。本当にそれが事実なのか、きちんと考えるには統計学が必要なのです。
と書きつつ、ぼくは実は統計学を体系的に勉強したことがありません。何回か始めようとしましたが、難しいのですね。しかも他の分野の難しさとは違う感じ……。やってみたいとは思っているのです……。
次の本は易しく、分かりやすく統計学を教えてくれます。カイ2乗検定も説明されています。ぼくにとって初めてのきちんとした統計の本で、とにかく面白かったです。工夫されており、高校生でも読むことができます。
