前、平均点に差があれば実力に差があると考えてよいのか、考えました。そこでは等分散を仮定できない場合について書きました。
そして、分散が等しいと考えてよいのかどうか検定する方法もまとめました。
最後に今回、上の検定(F検定)で等分散と判断してよいことが分かったとき、平均点に違いがあるかどうか検定する方法を整理しておきましょう。Excelを使います。
「2クラスで実施他試験の平均点に……」で使ったデータをまた使います。
1組は
53
62
57
53
53
34
70
63
49
で、平均54.9
2組は
58
40
26
50
48
50
55
45
43
48
52
40
で、平均46.3でした。
まず、等分散と考えてよいのか、調べます。
FINV(0.025, 8, 11) = 3.66381903428787
分散は順に 103.861111111111, 71.1136363636364
分散の比は 103.861111111111 / 71.1136363636364 = 1.46049501083
よって 分散の比<FINV(0.025, 8, 11) であり、分散は等しいと考えます。
続いてt検定に進みます。
データ → データ分析 → 「t検定:等分散を仮定した2標本による検定」
と進みます。
変数1の入力範囲、変数2の入力範囲をセットし、αには有意水準の0.05を入れ、出力先を適当に決めます。他はいじらず、OKをクリックします。結果は以下のようになりました。
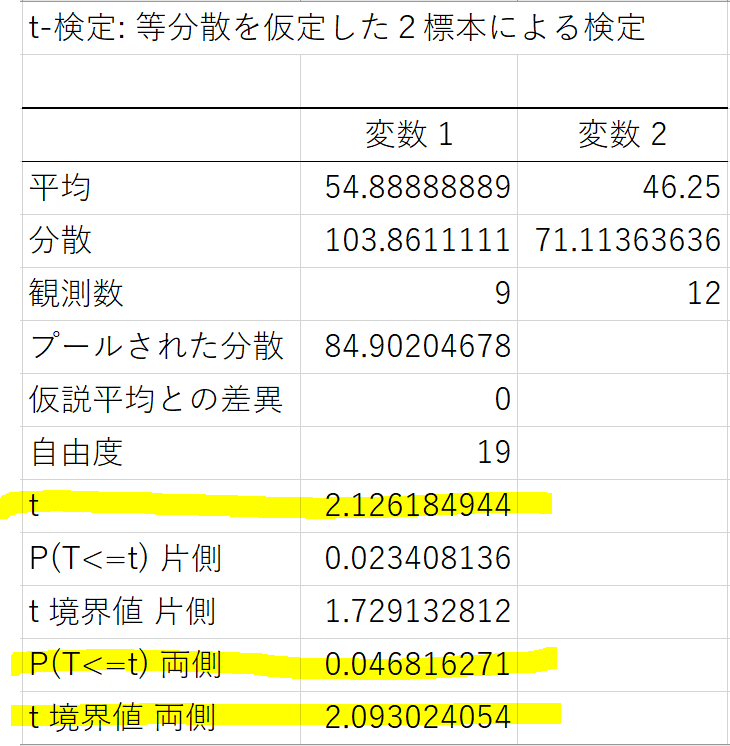
帰無仮説は「平均点は等しい」です。ここでは両側検定を使う(理由は前のt検定の記事を参照)ので、マーカーのところを見てください。|t|と「t 境界値 両側」を比較します。|t|<「t 境界値 両側」となっていますので、仮説は棄却されます。すなわち、「平均点は等しいとは言えない」が結論です。あるいは、下から2行目の「P(T<=t)両側」が有意水準の0.05未満なので仮説は棄却、と言っても同じです。
同じt検定はExcelのT.TEST関数を使ってもできます。
T.TEST(データの範囲1, データの範囲2, 2, 2)
で値を求めます。これで「両側p値」が求まります。データの範囲1、データの範囲2は2クラス分のデータの範囲を入れます。続く「2,2」は順に「両側確率」、「等分散を仮定」を意味します。上のデータで試してみると
T.TEST(データの範囲1, データの範囲2, 2, 2) = 0.0468162713880045
です。これは有意水準の0.05未満ですので仮説は棄却されます。ちなみに、このT.TESTの値は上の分析ツールの表の下から2行目、「P(T<=t)両側」に一致しています。
最後に平均点に違いがあるのか、検定する手順を簡単にまとめます。
①分散が異なるのか等しいのか調べます。
ブログの「等分散の検定」です。
②分散が等しいと仮定してよい場合
この記事の方法を使います。
③分散が等しいと仮定できない場合
ブログの「試験の平均点に差があったら実力は違うと考えてよいのか?」を使います。
一応スッキリしました。情報はあちこちバラバラに保存されているとあまり役に立ちません。どういう条件でどういう手順ならうまくいくのか、使えるカードを増やすことは大事だと思います。老練な職人が自分の道具を手入れするようなもの。プログラミングで言う「snippet」と同じです。「こういう目的のとき、こうしたらうまく動いた」というコードの小さなサンプルをまとめておきます。あとはこれらを有機的に組み合わせるのです。数学にも共通の部分があります。