生徒に聞かれました。教科書の問題です。関数が増加、減少している区間を答えなさい、というものです。
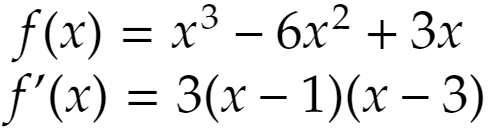
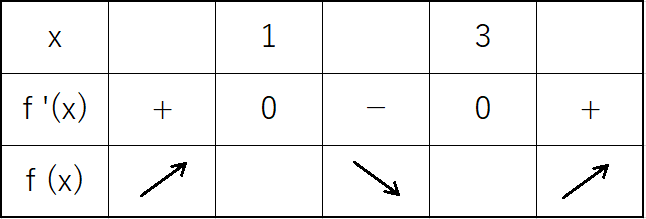
教科書の答えでは
です。生徒は「x=1、3では導関数の値が0なのに、増加や減少していると言っていいんですか」と。なるほど。
でも、教科書が正しいのです。そもそも関数が増加するとはどういうことか。次のように定義されています。数学Ⅰに出てきます。
関数y=f(x)は区間Iで(単調に)増加するとは、区間Iの任意の点s、tに対して、s<tならばf(s)<f(t)が成立することである。
区間Iとして、x≦1をとれば先の関数はIで増加であることはすぐ分かります。Iから-2,0.3を選んでも、-3,1を選んでも、確かにf(s)<f(t)が言えるでしょう。
要するに、導関数の値がどうだから増加、と定義されているわけではないのです。導関数の値がある区間でずっと正ならその区間では増加です。証明できます。
しかし、それとこれとは別の話です。導関数の値とは関係なく関数の増加、減少が定義されているのです。
状況によりますが一応、この話は授業のときにすることにしています。教科書では「x=1では導関数の値は0だが、関数が増加する区間に入れる」みたいに書いてあるだけです。これでは疑問に思う生徒が出てくるでしょう。多分こういう質問をする生徒は数学が好きなのだと思います。きちんとしたいから質問してくるのです。褒めてあげましょう!!