高校の数学Ⅱで相加平均、相乗平均というのが出てきます。足して2で割るなら分かるけど、かけ算してルートを計算って、何の意味があるんでしょうか。ある先生が「縦横2,8の長方形の面積は16。同じ面積の正方形は一辺√16=4。そういう意味で2,8の一種の平均を4と考える」という説明をしていました。それもありでしょう。
ラの音は440Hz(ヘルツ。1秒間の振動の回数、周波数の単位)で、1オクターブ上のラなら880Hz。周波数が高い音は高く聞こえます。ピアノなどの楽器を考えましょう。ラの次の音は半音上のラ#(ラのシャープ)、次がシ、ド、ド#、……と続きます。半音というのはピアノの白鍵とその隣の黒鍵までの周波数の差(音の高さの差)です。ラから1オクターブ高いラまでは440Hz、これは半音12個分です。すると半音1個分は? 440÷12=36.67Hzではありません。
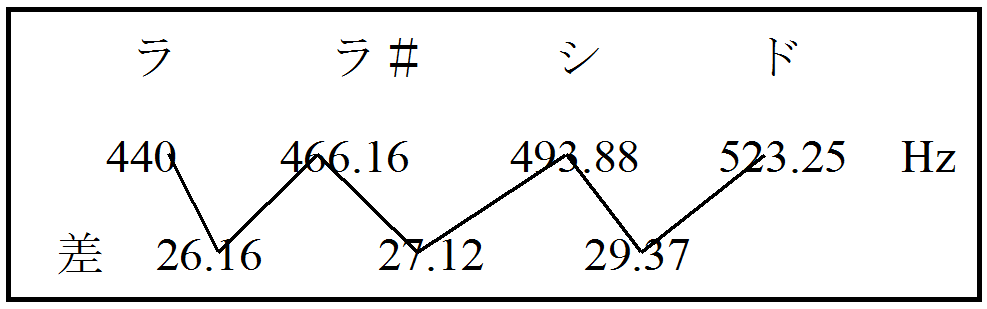
上のようになっており、差は一定ではありません。実はラ、ラ#、シ、……の周波数の列は等比数列になっていて、公比はだいたい1.059463094です。これは12乗すると2になる数です(この値を「2の12乗根」と言います)。つまり440×1.059463094×1.059463094×1.059463094×……×1.059463094(12回かけた)=880Hz(1オクターブ上のラ)となるのです。1.059463094を1回かけるたびに半音高い音になります。順にラ#、シ、ド、………、(1オクターブ高い)ラ、と得られるのです。このとき、人間の耳でラとシのちょうど真ん中に聞こえる音はラ#ですが、ラ#の周波数はラとシの相加平均ではなく、相乗平均なのです。実際、
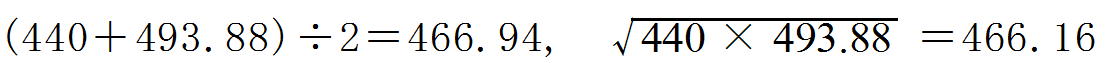
となっています。
「相乗平均なんて世の中で使われていない」と思っている人がいるかも知れませんが、とんでもありません。身の回りにも等比数列はたくさんありますが、等比数列から引き続く3項取り出すと1項目と3項目の相乗平均が2項目になるのです(各項は正とします)。等比数列が3項あれば、真ん中の項は左右の項の相乗平均なのです。