とにかく人間は忘れる動物です。プログラミングでは顕著です。コンピュータのブログラムは知恵を絞って時間をかけて、がんばって書くのですが数日で細かいことはきれいに忘れてしまいます。数ヶ月経っても何となくは憶えているので、そこがタチの悪いところです。分かっているつもりでも、何かやろうとしたときに「あれ?」という感じなのです。いくつかは、忘れないように、という意味も込めてブログに載せています。すでに何回か役に立っています。一応公開ですからそれなりにピリッとした感覚で書きますし、コードにコメントも普通以上につけたり、説明も載せたり。こうしてまとめておくと、とりあえずまともに動くコードであることは分かっていますし、その点は安心です。これは大事なことです。その上で「ここ、どういう意味なんだっけ?」など、ゆっくり考えればよいのです。
数学も近い部分はあります。自分で理解した事実はまとめておき、定理もどういう条件でどう使うのか、例でもつけておけば後で必要になったときに時間を節約できます。今回、少し書いてみようかな……と思った四元数は、1、2年前にいったん自分で理解したはずだったのですが細かな部分はすっかり忘れてしまっていたもの。ちゃんとブログに残します! 四元数は空間内の回転で点がどこに移るかの計算に使えるのですが、さしあたりその辺を。
空間内の回転には四元数の他、行列を使う方法もあります。ベクトル解析の理論も使えます。しかし『3次元回転』(金谷健一2019共立出版)によると、四元数は現在、大学でもほとんど扱われなくなったとのこと。10年以上前ですが、ぼくも3Dのシューティングゲームを書いたときには四元数ではなく行列を使いました。それでも四元数には意味があります。例えば、3次元の立体復元でE行列から回転の行列Rを求めるときなどに使えるのです(『3次元ビジョン』(徐剛、辻三郎1998共立出版))。
さて、前置きはここまで。今回は定義だけにしておきます。
i,j,kは虚数単位ですが互いに異なるもので、次が成立するものとします。
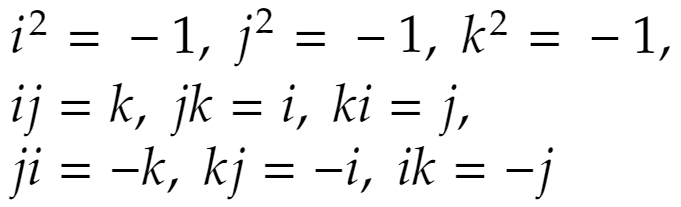
このとき、次のqを四元数と言います。
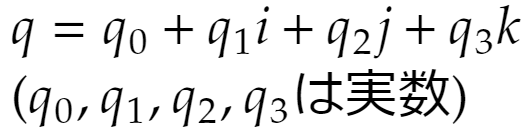
これはベクトルを使って次のようにも書かれます。
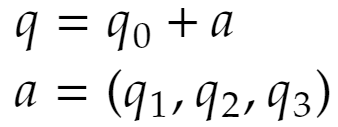
複素数を定義したときのような感じですね。定義の式に出てきている「+」は新しい数「四元数」を定義する際に使っていているわけで、どういう意味なのか明確ではありません。しかし複素数のときにはあまり気にしなかったはずです。
今回も気にせず、議論を進めましょう。四元数なるものがちゃんと存在して、四則も複素数みたいにできて、……ととりあえず考えるのです。回転の方法を調べることが目的です。