写真から立体を再現（8）　再び特異値分解(SVD)してみる

　特異値分解の理解を確実なものにするため、サイズの違う行列で試してみます。前回にも書いたとおり、Python（Numpy）で特異値分解をした場合、結果の解釈がやや難しい部分があります。今回、行列は3×3、ランク2のものを使います。前回の表を再び載せておきます。
f:id:Inuosann:20200319211821p:plain:w400
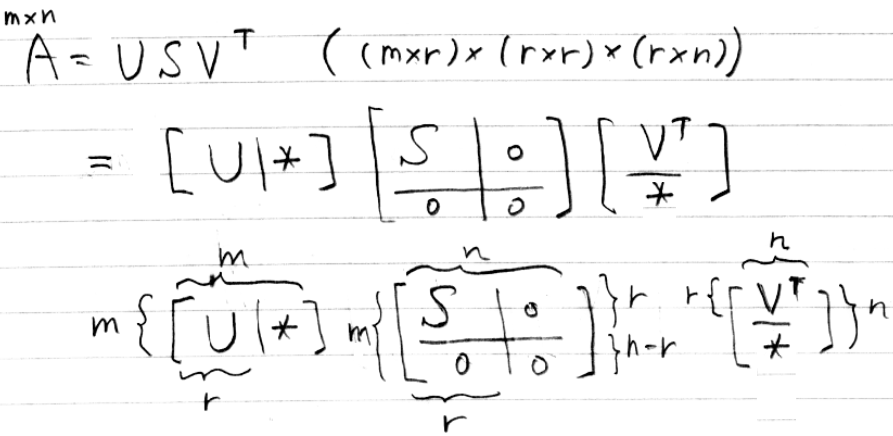
今回の例は m = 3, n = 3, r = 2 (ランク2) ですので、表で m - r = 1, n - r = 1 となることに注意して、結果を確認してください。

#========================================================
#特異値分解
#
import sys
import numpy as np
A = np.array([[3, 1, 2], [3, 2, 1], [0, 1, -1]])
U, S, VT = np.linalg.svd(A)
print('A = \n', A)
print('rank =  ', np.linalg.matrix_rank(A))
U, S, VT = np.linalg.svd(A) #特異値分解
print('U = \n', U)
print('S = \n', S)
print('VT = \n', VT)
S1 = S[0:2] #S[2]≒0なので、特異値はS[0], S[1]のみと判断
T = U[0:3, 0:2] #Uの1列目と2列目を取り出す
W = VT[0:2, 0:3] #VTの1行目と2行目を取り出す
B = np.dot(np.dot(T, np.diag(S1)), W) #かけ算して元に戻るか、確認
print('B = \n', B)
sys.exit()

　結果は以下の通りです。ランクは2ですが、特異値（正）が3つ求まっています。3つ目は絶対値がほぼ0なので、0と見なし、行列 S1 は S1 = diag(S[0], S[1]) として求めました（S1 は2つの特異値を対角成分に持つ、対角行列）。svd() の結果得られる U, S, VT から、上の表を見ながら U の1列目と2列目を取り出して T とし、先の説明のように S1 を作り、VT から1行目と2行目を取り出して W とします。B = T*S1*W が特異値分解の結果です。

A =
[[ 3 1 2]
[ 3 2 1]
[ 0 1 -1]]
rank = 2
U =
[[-7.07106781e-01 4.08248290e-01 5.77350269e-01]
[-7.07106781e-01 -4.08248290e-01 -5.77350269e-01]
[-2.46716228e-17 -8.16496581e-01 5.77350269e-01]]
S =
[5.19615242e+00 1.73205081e+00 1.17371774e-16]
VT =
[[-8.16496581e-01 -4.08248290e-01 -4.08248290e-01]
[ 1.01679661e-16 -7.07106781e-01 7.07106781e-01]
[ 5.77350269e-01 -5.77350269e-01 -5.77350269e-01]]
B =
[[ 3.00000000e+00 1.00000000e+00 2.00000000e+00]
[ 3.00000000e+00 2.00000000e+00 1.00000000e+00]
[-3.91239248e-17 1.00000000e+00 -1.00000000e+00]]