物理にニュートンリングというのがありました。平らなガラスと球面を持つガラスを接触させて上から単色光を当てます。これを上から眺めると、同心円状の明暗の模様が見えるのでした。具体的な模様の様子はネットですぐ見つかります。前から「これでいいのかな?」と疑問を持っていました。ご紹介します。
さて、下の図で同心円たちの半径がどうなるか簡単に計算してみます。当てる光の波長をλ、球の半径をR、同心円の半径をrとしておきましょう。rはいくつもあります。

見やすくするため、光線の経路を左右に少しずらして描いてあります。
△ODCで三平方の定理を使うと
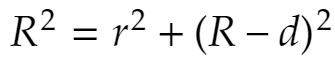
が成立します。r << R(rがRより極端に小さい)のとき、
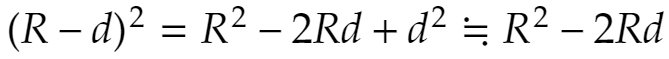
という近似式が成り立つので、先の式にこれを代入して
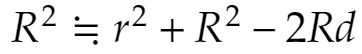
を得ます。よって
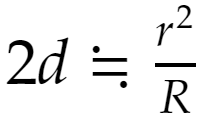
が言えました。必要なところを拡大しておきます。

Cで跳ね返る光とBで跳ね返る光があり、上から見るとこれらが干渉した結果の光が目に入ります。光の経路差は2dです。Bのところにニュートンリングの黒い縞が見えるとすると、2d=mλ(mは自然数)が成立します。波が強め合う条件です。ガラスの屈折率は1より大きく、Bで跳ね返る光は位相がπずれます(半波長分ずれる。固定端反射)。だから 2d=(m+1/2)λ でなく 2d=mλ なのでした。Cでは屈折率がガラスより小さな媒質(空気)で反射するので位相は変わりません(自由端反射)。これをさっき導いた式に代入すると
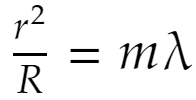
となり、従って
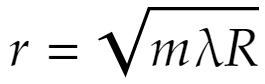
を得ます。これでニュートンリングの縞の半径が分かりました。
こういう理屈でこんなにハッキリ半径まで分かるのです。高校生だったぼくにはこういう話がとにかく面白く、物理が好きでした。ただ……当時から「いいのかな?」と何となく思っていました。図のCで光は屈折するはずです。入射角とガラスの屈折率でどの程度屈折するか決まるのでした。それを考慮に入れなくてもいいのでしょうか。可能性として、例えばガラスの面は水平に近く、屈折してもごくわずかだから無視してよいのだ、とか。この場合、半径を求める式が成立するのはDからあまり離れていないところに限ります。真相をご存じの方、いませんか??
今回、式変形などは前にも紹介したテキストに従いました(この問題に関してはどのテキストもたいていこんな感じだとは思いますが)。
公式の導出の過程もしっかり載っていますし確認テストもついています。新書版でコンパクト。楽しい本です。人間、どんなに勉強しても時間が経てば細かなことは(場合によっては細かくないことも!)ビックリするほどきれいに忘れます。勉強を進めるときに困りますから、こんな公式集があると助かります。
追記:
Cで反射する光も、真上には進まないはずですよね……。
