メネラウスの定理というのは以下のようなものでした。高校では数学Aで出てきます。三角形を直線が横切っているとき、次が成立します。
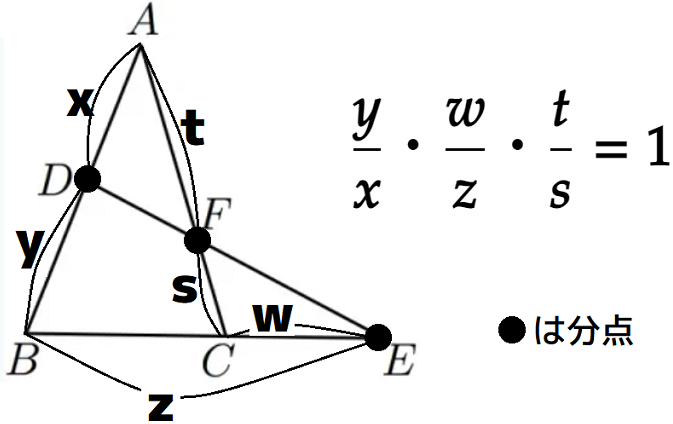
図では△ABCを直線DEが横切っています。証明や覚え方、例題などについてはよいサイトがたくさんあるので検索してみてください。ここではメネラウスの定理を使うときのちょっとした工夫を書きます。「自分はこの定理を使うとき、一切迷ったことはない!!」と言い切れる人にはこの記事は必要ありません。
例をあげましょう。
AD:DB=2:1、DF:FC=1:3のとき、BE:ECを求めてください。
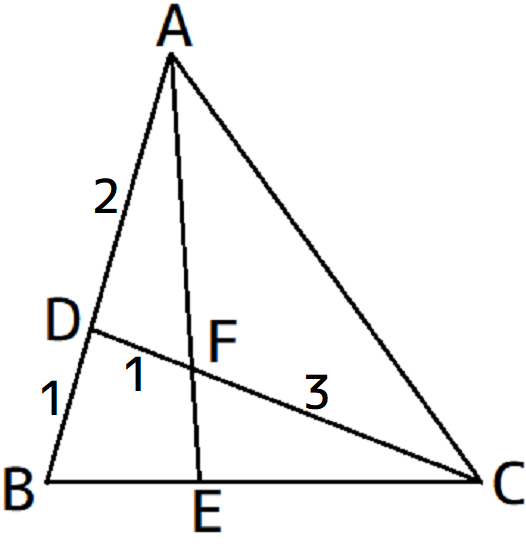
つまりこんな感じです。↓
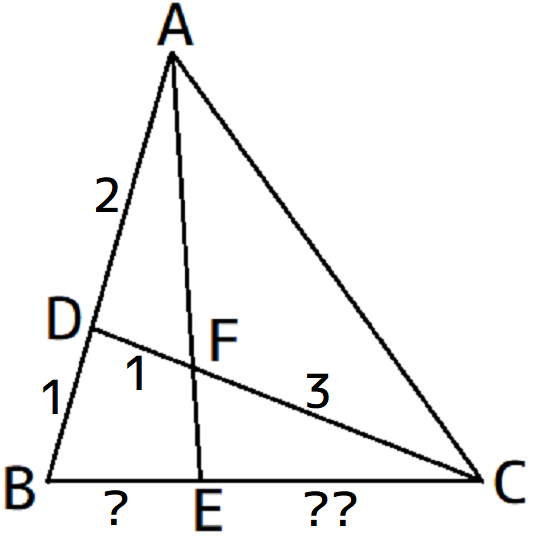
メネラウスの定理を使うときは、どの三角形をどの直線が横切っているのか分からないといけません。ここで、メネラウスの定理の問題では、比が出てきたらそれは辺(あるいはその延長)の上で測った比であることに注意しましょう。従って上の例題でメネラウスの定理を使うなら、AB、DC、BCが三角形の3辺になっているはずです。次の図を見てください。
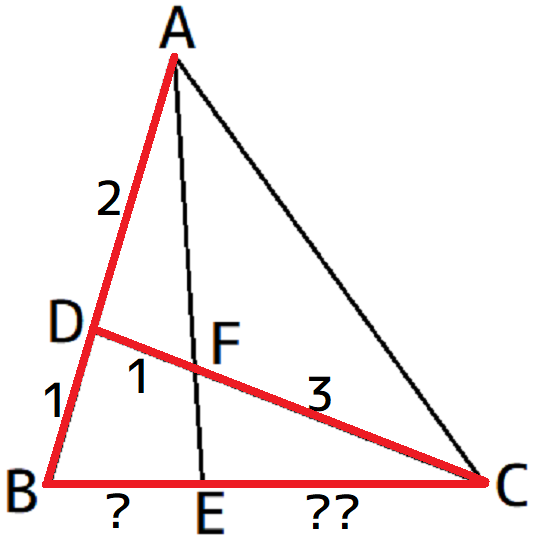
これで△DBCに対してメネラウスの定理を使えばよいのだ、と分かります。
問題に余分な情報が書いてあることもあります。そのときは結局また迷うことになりますが、それでもここで紹介した方法を使えば楽になるはずです。
今回書いたことは数学の本質とは関係ありませんよね。でも考えなければならないことはたくさんあるのです。簡単なルールで楽をできる部分では楽をしましょう!! そうすれば肝心なところに集中できるのです。