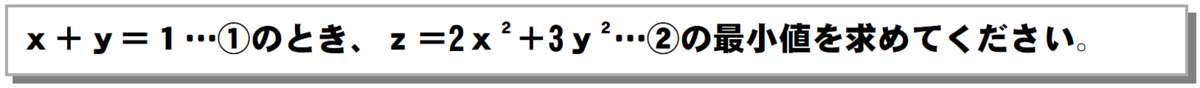
高校生がこの問題を解くなら、たいてい以下のようにやるでしょう。

あとは平方完成でもすればいいですね。しかし、①から③を導きましたが、今回は①が簡単だったのでそれでよかったのです。①の代わりにとかだったらどうしますか? つまり、1変数について解き、代入して変数を消去……という解き方が通用しないことだってあるわけです。今回は、こうした変数の消去を行わないで極値を求める方法を紹介しましょう。ラグランジュの未定乗数法と言います。偏微分という考え方が必要ですが、どうってことはありません。例えば
のとき、zをxで偏微分すると4xとなり、zをyで偏微分すると6yです。要するに「xで偏微分せよ」と言われたら、他の変数は定数だと思って今までの微分をするだけです。記号では
、
です。この偏微分の記号を使ってラグランジュの未定乗数法を説明すると以下の通り。

簡単でしょう? この解き方の中で、④が肝心な式です。④は、この分数の値をλ(ラムダ。ギリシャ文字です)とおけば となりますが、このλが「未定乗数法」の「未定乗数」なのです。どうしてこういう方法が使えるのか、その理屈は(図形的な証明でよければ)分かりやすいです。金谷先生の本に載っています。
これなら分かる最適化数学―基礎原理から計算手法まで
あと1題出しておきましょう。
-------------------------------
問.
長方形の周の長さはLで一定だとします。このとき、長方形の面積の最大値を求めてください。
答.
長方形の縦、横をそれぞれx、yとするとL=2x+2y。そこで
w=2x+2y-Lとおきます。問題の条件「周が一定」はw=0(2x+2y-L=0)と書けます。面積をz=xyとすると、ラグランジュの未定乗数法によれば
です。これに
を代入すると y/2=x/2 ゆえにx=y。これと2x+2y-L=0を連立して、2x+2x-L=0 よってx=L/4。これで面積の極値はx=y=L/4のときで、
と分かりました。
-------------------------------
実はラグランジュの未定乗数法で分かるのは極値の候補であって、実際にそれが極値になるかどうか(もちろんそれが最大値や最小値であることも)は別途検討する必要があります。しかし例えば後半の問題では問題の性質上、どこかで最大になることは明らかと言ってよいですから、最後の答えは最大値です。