今回、「ルート2」を「√2」と書いてしまうことにします。√2 ≒ 1.41421456(一夜一夜にひとみごろ)、√3 ≒ 1.7320508(人並みにおごれや)なのでした。では√2.5は? だいたいの値でいいです。今は100均でルートキー付きの電卓が買えるし、スマホならルートキーも使えるでしょう。でもルートキーは使わないで計算してみることにしましょう。
いい方法があります。√2.5 は多分 √2 と √3 の真ん中くらいでしょう。そこで、√2.5 ≒(√2 +√3)/2 ≒(1.41421456+1.7320508)/2 ≒ 1.57313218。実際の値は、ちゃんと√キーで計算すると√2.5 ≒ 1.58113883 だから、うーん、まあまあか? 2と3の間はかなり離れているからこんな結果になったんでしょう。
それなら……√2 ≒ 1.41421356、√2.3 ≒ 1.516575089 を使っていいことにして(これらの値は与えられているとする)、ルートキーは使わずに√2.17 のだいたいの値を求めてみましょう。
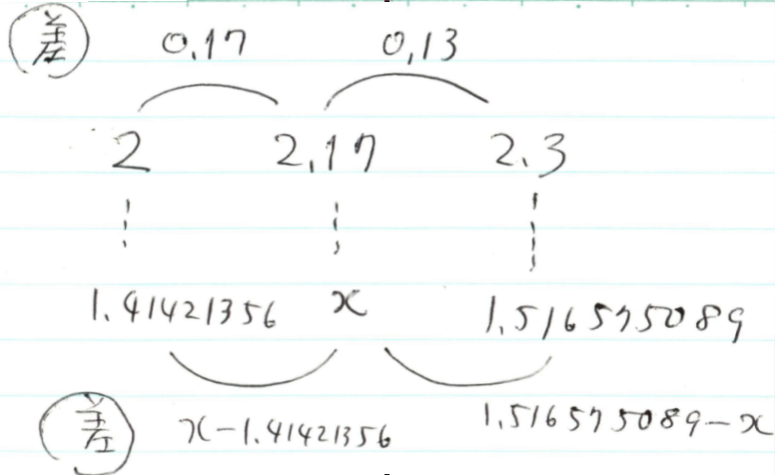
上の図から
x-1.4142156:1.516575089-x=0.17:0.13。内項と外項の積は等しいので
(1.516575089-x)× 0.17=(x-1.4142156)× 0.13。展開して
0.2578177651-0.17x=0.13x-0.1838477628。これより
0.3x=0.4416655279、よってx=1.472218426。実際には√2.17 ≒ 1.473091986なので、なかなかです! この方法は補間法と言います。
実際には最初に書いたように今はいい電卓が大変安く手に入りますから、こんなことをする価値はないように思えるかも知れません。そこで、こういう計算が必要な例をお見せしましょう。
例えば日の出の時刻の計算のときには地球と太陽の距離が必要です。太陽が遠ければ小さく見えますよね。日の出というのは「太陽の輪郭線の上部が地平線に達した瞬間」と定義されているので、太陽の見かけの大きさは日の出の時刻に直に関わるわけです。実は太陽は時刻によって地球に近づいたり地球から離れたりしています。ケプラーの第1法則によれば地球は太陽を焦点とする楕円軌道を描きます。円軌道でないため、季節により距離が変わってしまうのです。下は何年か前の理科年表の一部です。6月の太陽の位置、地球との距離などが載っています。「距離」の欄を見て下さい。6月16日の距離は1.01577、6月20日は1.01612です(どちらも世界時0時、つまり日本時で9時の値です)。ここで、距離の単位はauです。これは「天文単位」とも言われ、主に太陽系内の距離を測るのに用いられます。現在では1au=149597870700mと定義されています(もともとの定義では地球と太陽の間の平均距離が1au、ということでした)。さて、今日、6月17日の太陽と地球の間の距離xを求めてみましょう。
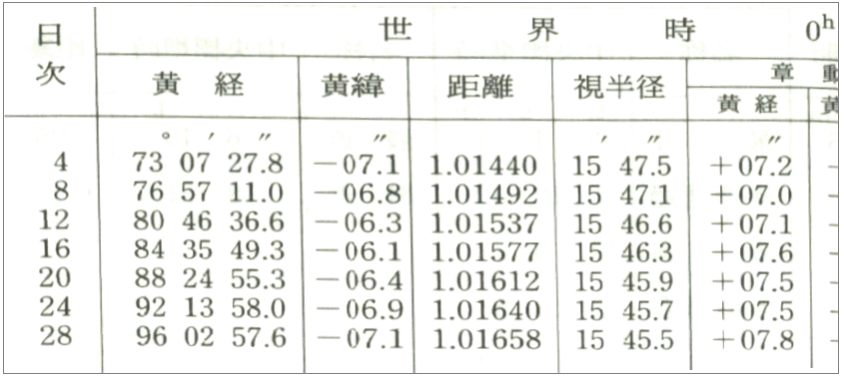
さっきと同じように、x-1.01577:1.01612-x=1:3という式を立てます。これより 1.01612-x=3x-3.04731。よって4x=4.06343。
よってx=1.0158575と分かりました! これは151970118.9kmにあたります。もちろん一定の割合で距離が変化している保証はありませんから、近似計算です。しかし計算はラクだしそれなりの精度が出るし、素晴らしい方法です! 理科年表にはご覧の通りで4日おきのデータしかありません。何かの方法で間接的に計算するしかないのです。なお、対象によっては2次式で近似することもあります。ここで紹介したのは1次式による近似です。
理科年表はすごいデータブックです。利用にはちゃんとした知識が必要な部分もありますが(さっきの「太陽と地球の距離」とか)、たったの¥1540で凄まじい量のデータが手に入ります。勉強すればこの本のデータを使って日の出・日の入りの時刻とか、蠍座のアンタレスが何時にどこに見えるとか、計算することもできるのです。
