2004年、アメリカのシリコンバレーの高速道路脇に「{first 10-digit prime found in consecutive digits of e}.com」という看板が出たそうです。日本語に訳すと「{自然対数の底(てい)eの中の連続する10桁の最初の素数}.com」です。少し意味が取りづらいかも知れませんので説明しましょう。素数というのは1と自分自身でしか割り切れない自然数のことでした(ただし1は素数でないと約束します)。例えば7は素数ですが、6は素数ではありません(2や3で割り切れるから)。自然対数の底eというのは、数学Ⅲで出てくる、とある定数です。無理数で、具体的な値は以下の通り。値が必要なだけなので、今はこの数値の意味は分からなくても大丈夫です。
e=2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274274663919320030599218174135966290435729003342952605956307381323286279434907632338298807531952510190……(以下、無限に続く。この値はネットで見つけました)
先頭の10桁は2718281828です。これは素数ではありません。末位が2なので偶数、つまり2で割り切れるからです。1桁ずらすと7182818284ですが、これも素数ではありません。また1桁ずらすと……と、これを繰り返して、初めて10桁の数が素数になったら、それが看板の「自然対数の底eの中の連続する10桁の最初の素数」です。実は小数第99位から10桁分の7427466391が初めての素数なので、看板は「7427466391.com」という、どこかのサイトのアドレスを示していることになります。
実はこれ、Google(インターネットの、検索サイトのあのグーグル)の社員募集の広告でした。『グーグル革命の衝撃』(NHKスペシャル取材班2009新潮文庫)で読みました。NHK取材班がグーグル本社に乗り込み、グーグルがどんな会社なのか、グーグルの人たちが何を考えているのか、明らかにします。TVでも放送されました。
さて、「7427466391.com」というサイトのアドレスが看板に載っていたのでした。ブラウザ(インターネットエクスプローラとか)のアドレス欄にこれを入れてEnterを押せばグーグルが用意したサイトにつながります。面白いこと考えるなあ……。問題もそうだけれど、こういう広告の仕方です。看板自体には「Google」とは書いてないので、問題を解いてサイトにたどり着かなければグーグルの広告であることすら分かりません。グーグルはそもそもまず、こういった問題の内容を理解し、興味を持つ人間を欲しがるわけです。そしてそれだけではダメで、この問題を解けることが必要だということです。グーグルはこういう募集について、ブログで「グーグルはいつも我々が発見しうる最も優秀なエンジニアを雇いたいと考えており、こうした方法はそのために開発したものだ」とコメントしているそうです。
では問題を考えてみましょう。どっち道この問題はコンピュータなしでは解けないのですが、まずeの値の求め方。eの値はネットでも、本からでもすぐ手に入ります。そうでないとeをある程度の桁まで自分で(パソコンを使って)計算しないといけません。そのつもりならeは下の式で計算できますが、すぐに有効桁数の問題にぶつかります(「!」は「階乗(かいじょう)」と読む。例えば4!=4・3・2・1と計算するのでした)。
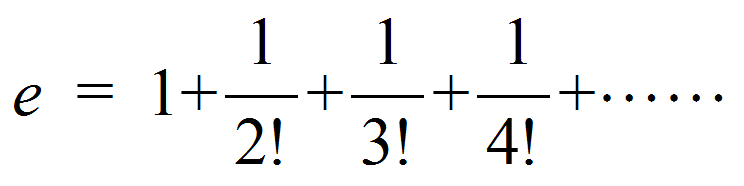
何かのプログラミング言語を使うことになりますが、何を使ってもたいてい、普通のやり方ではせいぜい10桁か20桁までしか扱えません(x=2.71828182845904523 というように変数に細かな値を代入しても、途中で打ち切られてx=2.718281828にしかならない、など)。グーグルの問題の答の素数は先に書いたとおりで小数第99位から10桁分ですから、最低でもeの小数第110位かそこらまでは分かっていないとこの問題は解けないのです。有効桁数が10桁しかなくても、小数第200位まででも300位まででも求める方法はあります。『パソコンで挑む円周率』(大野栄一1991講談社ブルーバックス)で説明されています。これはこれですごく面白い話なんですが、eの値はネットで手に入れるのが楽でしょう。
さて、そうしたら今度は「どの10桁が素数か?」ということになります。パソコンでeの1桁目から10桁分(2718281828)が素数かどうかをチェックし、それが素数でなかったら2桁目から10桁分(7182818284)をチェックし、それが素数でなかったら3桁目から10桁分(1828182845)をチェックし……とやっていけばいずれ正解にたどり着けます。今回はまあ10桁だし一番原始的な方法で十分でしょう。「2で割り切れたら素数ではない。あとは3,5,7,…と順に奇数で割って、途中で割り切れたら素数ではない」で分かります。なお、「自然数nが素数でないなら、nは素因数を√n以下の範囲に持つ」という定理があるので(証明は高校数学の範囲です)、これを利用すればある程度ラクをできます。あるいは、片っ端から「2718281828.com」、「7182818284.com」、「1828182845.com」、……と試していけばいずれは当たるけれど、手作業では大変すぎますよね(100回やる気力ありますか? それも100回で終わる保証もないのに……)。でも自分でプログラムを書いてパソコンにやらせるなら、それでもいいでしょう。この場合はeの値から必要な部分を取り出し、「1828182845.com」などのアドレスを作り、そのアドレスに接続する手続きを実行、を繰り返すことになるでしょう。これはこれで一応技術が必要だし、そうやって正解にたどり着いてもグーグルはきっと歓迎してくれるはずです!

